5. QUANTUM HYDRODYNAMIC FLOWS
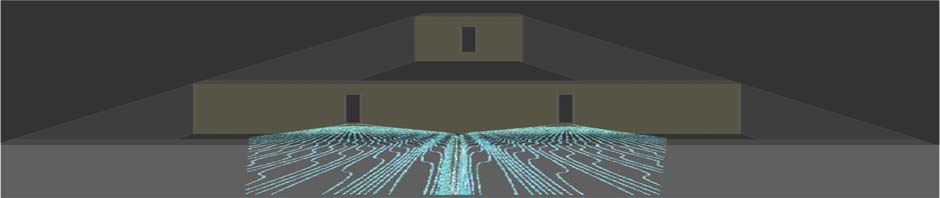
The Bohm picture may also be viewed as a quantum hydrodynamic picture as foreseen by Madelung [39]. In the quantum transport modelling of devices whether by solving the time dependent Schrödinger equation or by the full power of non-equilibrium Green’s function (NEGF) methodology, a well-defined charge density and current density may be computed with the aid of Poisson’s equation from which device modellers extract the current-voltage characteristics. A velocity field may be extracted from the ratio of current density to the charge density. The resulting density field, velocity field pair may be energy resolved in steady state problems or may be computed for the macroscopic density and velocity fields. This construction is essentially a post-processing method that reveals trajectories (in Bohmian view) or streamlines (quantum hydrodynamic view). We have performed extensive studies of quantum transport in realistic nano-devices (where one assumes the presence of non-self-averaging) atomistic micro-variability using this approach under-pinned by NEGF methods [28-29, 40-59]. An approach to a full many body field theoretic quantum hydrodynamics is outlined in [66]