Quantum Trajectories in Nanoelectronics-a short review
1. INTRODUCTION
The study of quantum transport in semiconductor devices, particularly in nano-structured systems, has benefited from the interpretive power of the concept of quantum trajectories either in direct space or in phase-space.
The Boltzmann-Bloch electron transport picture which is widely used in device modelling pre-supposes the existence of electron trajectories. Not only does this aid physical intuition on transport theory but it also opens the door to powerful computational techniques from hydrodynamic models to ensemble Monte Carlo.
Quantum transport theory has similarly blossomed when some kind of trajectory picture has been made possible, for example with the existence of edge states in high magnetic field, or in quadratic potential fields for which the Wigner distributions provide classical flowlines. Generally, however, the existence of interference, diffraction and tunnelling phenomena brings out the wave- or rather field-theoretic nature of quantum transport and the simplifying classical picture is lost. In hot electron theory this has been particularly acute for phenomena such as the intra-collisional field effect and other consequences of extended collisions. Although the Feynman formulation of quantum mechanics involves paths for electrons, it is their integration into a final field which is significant and the existence of the uncertainty relations and more seriously the known non-locality of quantum mechanics would seem to rule out the existence of a genuine phase-space trajectory for an electron. In fact this is not at all obvious; as first pointed out by Bohm an interpretation of quantum mechanics is possible in which electron trajectories not only exist but evolve deterministically under classical forces plus a quantum force which derives from a complicated dependence on the intensity of the wavefunction (itself represented as a real physical field-the pilot field) .
In the Bohm picture the electron momentum at any position in the pilot field is given by the gradient of the phase of the field.What makes the Bohm picture of current interest is the new possibility for manipulating individual electrons within tightly controlled geometries with injection from single-electronics systems based on ultra-small capacitative structures. This has led to renewed interest in conceptual tools for describing individual electrons.
Our studies concern a critical re-evaluation of the Bohm picture as a transport theory and show that although it can be significantly reconciled with orthodox quantum transport theory it still contains serious flaws in its description of the initial value problem, non-integrable phase problems, stationary bound states, deterministic trajectories and the handling of electron transit/tunnelling times. The root cause of the problems is the initial condition in the Bohm picture: to determine an electron trajectory one must select its initial location with a probability given by the conventional quantum probability density for locating the electron in space; thereafter, the electron dynamics evolves deterministically. We have shown that a re-interpretation of the Bohm picture exists, based on a different deconstruction of the Schrodinger equation, for which these problems appear to be resolved. Individual electron trajectories occur, but they are stochastic and Bohms result represents the mean trajectory.The main problem with these approaches is that in general they involve post-processing: the trajectories may be calculated only after a full quantum state is computed.There are situations where this can be avoided. For instance the drift-diffusion theory of classical device modelling may be extended with the aid of Poisson’s equation coupled to the quantum potential to obtain direct solutions of some problems. Where such approaches succeed is when the phase of the wavefunction is constant. Otherwise the phase contributes quantised anular momentum states, vortex flows and other phenomena that cannot be constructed from drift-diffusion-quantum potential (or density gradient) schemes.
In most cases of interest the Bohm picture is better understood in terrms of quantum hydrodynamics where the density-current density formalism leads to flowlines rather than particle trajectories. Quantum hydrodynamic flows are most rigorousl obtained from non-equilibrium (Keldysh) Green’s function methods.
In the following we briefly review our contributions and general progress since the 1980s.
2. WAVE-PACKET TRAJECTORIES AND TRAVERSAL TIMES
The simple classical notion of a particle arriving at a particular place at a particular time is problematic in quantum mechanics and led to considerable practical interest in the concept of a tunnelling time [1]. The rapid development of novel quantum devices that exploited semiconductor heterostructures, such as resonant tunnelling diodes, led to several detailed studies of the traversal time problem based on generating trajectories derived from monitoring features of scattered wave-packets obtained from direct solution of the time-dependent Schrödinger equation [2-5]. Further interest followed the advent of single-electron devices [6-9]. The concept of traversal/tunnelling time was reviewed under the PHANTOMS programme [10] and has been resurrected again [11] in studies of SiGe devices and in the context of experimental data in [12].
3. BOHMIAN TRAJECTORIES
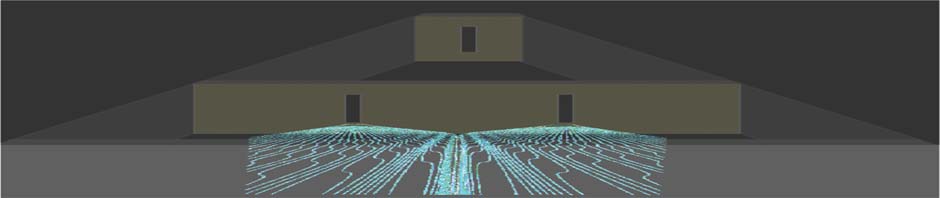
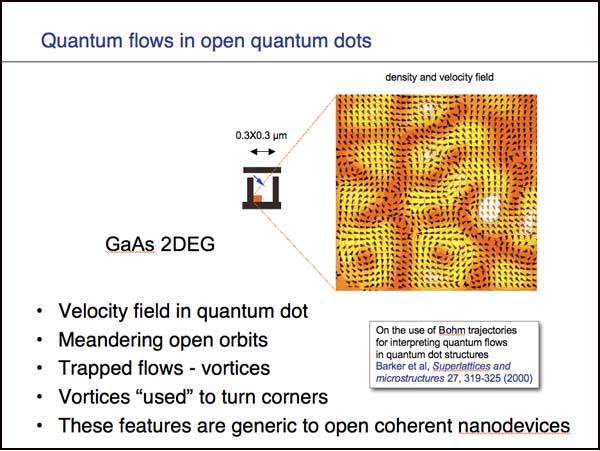
For many years the theory of quantum transport in nanostructures has benefited from the interpretive power of Bohmian trajectories [13] by the post-processing [11, 14-29] of direct quantum calculations for either wave-functions or non-equilibrium Green’s Functions . The resulting trajectories are deterministic [20] with interesting topological properties. Non-deterministic trajectories have also been advocated in an extension of Bohmian mechanics to a stochastic form but have had limited application. The possibilities for using ab initio Bohmian mechanics as a direct self-contained simulation tool has been discussed in the light of modern semiconductor device simulation but runs into difficulties when vortex motion occurs [20, 23]. Time-dependent studies of transport in semiconductor quantum waveguide structures have revealed a rich source of vortex flows corresponding to highly complex quantum potentials [24].
The Bohm picture has also proved useful in interpreting novel logic devices that rely on non-invasive measurement [25].
4. QUANTUM POTENTIAL/DENSITY GRADIENT
In modern semiconductor device modelling many groups now routinely use the Quantum Potential or Density Gradient as a calibratable function for incorporating effects of quantum confinement, quantum transport and tunnelling within ab initio drift-diffusion modelling [29-36] where the band structure may have a profound impact [23, 36, 65] on the standard form [13] of the quantum potential. This approach generally compares quite well with full non-equilibrium Green function methodology except where macro-vortex formation occurs. As with any attempt to forward integrate the Bohmian equations of motion there are difficulties when strong vortex flows occur because the quantisation of vorticity stems from an integrability condition on the phase [20]. However, there are severe limitations to using the quantum potential alone, particularly if vortex motion is present in the current flow. It is then not possible to derive the velocity field from the carrier density alone (through the continuity equation) because the flow is not irrotational. Generalisations, based on gauge invariance, to include a quantum vector potential[37] have been suggested and explicit examples constructed. These simple pictures have been corroborated by full self-consistent Non-Equilibrium Green’s function studies of nano-structured devices where the quantum hydrodynamic velocity field is obtained directly(reviewed [29]). Various important generalisations of the quantum potential are reviewed in [38].