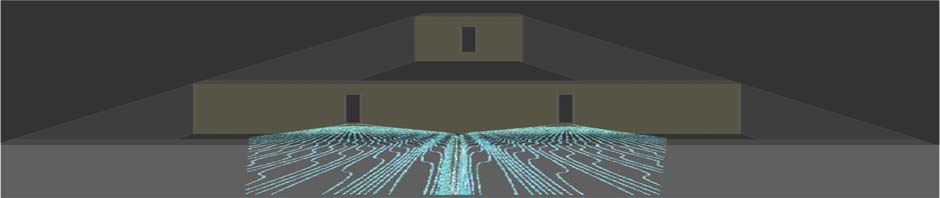
The header picture is a schematic based on a calculation of Bohm trajectories for particles (photons or electrons) exiting a two-slit interferometer (from a lecture given to the Glasgow Science Festival 2010- J R Barker “The Smile on the Face of the Quantum”)
NEWSFLASH! (3rd June 2011) What appears to be the first experimental evidence for Bohm trajectories is shown in a recent paper in Science:
see page 2 below
Quantum trajectories are the hypothetical paths followed in space and time by elementary particles. Their existence is highly controversial! According to orthodox Physics the Heisenberg uncertainty relations imply that the position and momentum of a particle are not simultaneously observable. Existence of a well-defined trajectory in space-time would imply a definite momentum at each position which apparently contradicts quantum mechanics. However David Bohm (1952) first showed that an interpretation of quantum mechanics exists in which a particle in a given quantum state (described by a wave function obeying Schrodinger’s equation) exists on one of many possible deterministic trajectories for which the momentum is given by the gradient of the phase of the wave function at that point. In this picture the wave function is a real field which accompanies and pilots a particular particle-a view first hypothesized by de Broglie. The Bohm-de Broglie picture is useful for interpreting flows of particles when a conventional quantum mechanical solution (e.g for a wave function) is known. A small subset of physicists (including me) believe there is considerable merit in the Bohm interpretation of quantum mechanics although I have always held the view that the Bohm trajectories are not deterministic “actual” trajectories but rather ensemble averages of underlying stochastic trajectories. There are other well established ideas about quantum trajectories some of which I summarise below.
NEWSFLASH! (3rd June 2011)
What appears to be the first experimental evidence for Bohm trajectories is shown in a recent paper in Science: see page 2 below