9. Origin of quantum vortices
In the simplest picture suppose just consider a single electron moving in a general potential energy field. Quantum mechanics allows us to compute the probability density n(r,t) for the position of the electron and also the particle current density j(r,t). The velocity field v(r,t) corresponding to the density field may be defined as v=j/n. In cases where we can define a wave function the velocity is just the gradient of the phase of the wave function divided by the electron effective mass (actually this result is not generic it depends on the intrinsic relation between momentum and velocity which is non-trivial in electron assemblies in condensed matter). In our work we compute velocity via non-equilibrium Green functions.
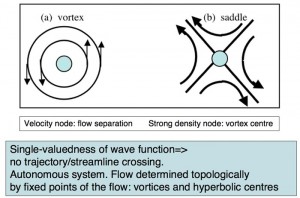
In coherent systems the quantum hydrodynamics defined by the scalar and vector fields n(r,t) and v(r,t) have steady flows defined topologically by a usually small number of singular points in the flow. These correspond to hyperbolic point where flows separate and vortex points where the flow circulates in closed paths. These properties follow from a theorem that the quantum streamlines cannot cross except at a singular point: a consequence of the single-valuedness of the wave function. Vortices are associated with strong nodes in the density where the density becomes vanishingly small. Hyperbolic flow occur at points where the velocity field vanishes. Interestingly, all the vortex types seen in classical hydrodynamics also occur in quantum hydrodynamics.
Next: examples of quantum vortices